Here are some common terms used in digital electronics:
- Digital systems are used in almost all aspects of life, incommunications, business transactions, traffic control, medical treatment, the internet…etc.
- Digital logic is the first course in studying digital systems, which is an essential part of almost all branches of Electrical Engineering.
- Logical–refers to a signal or device in terms of its meaning, such as "TRUE" or "FALSE"
- Physical–refers to a signal in terms of voltage or current or a device’s physical characteristics
- HIGH–the signal level with the greater voltage • LOW–the signal level with the lower voltage
- TRUE or 1–the signal level that results from logic conditions being met
- FALSE or 0–the signal level that results from logic conditions not being met.
- Active High–a HIGH signal indicates that a logical condition is occurring
- Active Low–a LOW signal indicates that a logical condition is occurring
- Truth Table–a table showing the logical operation of a device’s outputs based on the device’s inputs
- State–a stable combination of signals or of a set of inputs and outputs, can refer to a device, a circuit, or a set of signals
Number Systems
Digital logic may work with “1s and 0s”, but it combines them into several different groupings that form different number systems. You’re familiar with the decimal system, of course. That’s a base-10 system in which each digit represents a power of ten. In the field of logic you’ll also encounter…
• Binary–base two (each bit represents a power of two), digits are 0 and 1, numbers are denoted with a ‘B’ or ‘b’ at the end, such as 01001101B (77 in the decimal system)
• Hexadecimal or ‘Hex’–base 16 (each digit represents a power of 16), digits are 0 through 9 plus A-B-C-D-E-F representing 10-15, numbers are denoted with ‘0x’ at the beginning or ‘h’ at the end, such as 0x5A or 5Ah (90 in the decimal system) and require four binary bits each. A dollar sign preceding the number ($01BE) is sometimes used, as well.
• Binary-coded decimal or BCD–a four-bit number similar to hexadecimal, except that the decimal value of the number is limited to 0-9.
• Decimal–the usual number system. When used in combination with other numbering systems, decimal numbers are denoted with ‘d’ at the end, such as 23d.
• Octal–base eight (each digit represents a power of 8), digits are 0-7, and each requires three bits. Rarely used in modern designs.
Conversion Bet. Diff. Number Systems
Positional number systems
Our decimal number system is known as a positional number system, because the value of the number depends on the position of the digits. For example, the number 123 has a very different value than the number 321, although the same digits are used in both numbers.
(Although we are accustomed to our decimal number system, which is positional, other ancient number systems, such as the Egyptian number system were not positional, but rather used many additional symbols to represent larger values.)
In a positional number system, the value of each digit is determined by which place it appears in the full number. The lowest place value is the rightmost position, and each successive position to the left has a higher place value.
In our decimal number system, the rightmost position represents the "ones" column, the next position represents the "tens" column, the next position represents "hundreds", etc. Therefore, the number 123 represents 1 hundred and 2 tens and 3 ones, whereas the number 321 represents 3 hundreds and 2 tens and 1 one.
The values of each position correspond to powers of the base of the number system. So for our decimal number system, which uses base 10, the place values correspond to powers of 10:
| ... | 1000 | 100 | 10 | 1 |
| ... | 10^3 | 10^2 | 10^1 | 10^0 |
Converting from other number bases to decimal
Other number systems use different bases. The binary number system uses base 2, so the place values of the digits of a binary number correspond to powers of 2. For example, the value of the binary number 10011 is determined by computing the place value of each of the digits of the number:
| 1 | 0 | 0 | 1 | 1 | the binary number |
| 2^4 | 2^3 | 2^2 | 2^1 | 2^0 | place values |
So the binary number 10011 represents the value
| (1 * 2^4) | + | (0 * 2^3) | + | (0 * 2^2) | + | (1 * 2^1) | + | (1 * 2^0) | |
| = | 16 | + | 0 | + | 0 | + | 2 | + | 1 |
| = | 19 | ||||||||
The same principle applies to any number base. For example, the number 2132 base 5 corresponds to
| 2 | 1 | 3 | 2 | number in base 5 |
| 5^3 | 5^2 | 5^1 | 5^0 | place values |
So the value of the number is
| (2 * 5^3) | + | (1 * 5^2) | + | (3 * 5^1) | + | (2 * 5^0) | |
| = | (2 * 125) | + | (1 * 25) | + | (3 * 5) | + | (2 * 1) |
| = | 250 | + | 25 | + | 15 | + | 2 |
| = | 292 | ||||||
Converting from decimal to other number bases
In order to convert a decimal number into its representation in a different number base, we have to be able to express the number in terms of powers of the other base. For example, if we wish to convert the decimal number 100 to base 4, we must figure out how to express 100 as the sum of powers of 4.
| 100 | = | (1 * 64) | + | (2 * 16) | + | (1 * 4) | + | (0 * 1) | |
| = | (1 * 4^3) | + | (2 * 4^2) | + | (1 * 4^1) | + | (0 * 4^0) | ||
| Then we use the coefficients of the powers of 4 to form the number as represented in base 4: | |||||||||
| 100 | = | 1 2 1 0 | base 4 | ||||||
One way to do this is to repeatedly divide the decimal number by the base in which it is to be converted, until the quotient becomes zero. As the number is divided, the remainders - in reverse order - form the digits of the number in the other base.
Example: Convert the decimal number 82 to base 6:
| 82/6 | = | 13 | remainder 4 |
| 13/6 | = | 2 | remainder 1 |
| 2/6 | = | 0 | remainder 2 |
The answer is formed by taking the remainders in reverse order: 2 1 4 base 6.
LOGIC OPERATIONS AND TRUTH TABLES
Digital logic circuits handle data encoded in binary form, i.e. signals
that have only two values, 0 and 1.
Binary logic dealing with “true” and “false” comes in handy to describe
the behaviour of these circuits: 0 is usually associated with “false” and
1 with “true.”
Quite complex digital logic circuits (e.g. entire computers) can be built
using a few types of basic circuits called gates, each performing a single
elementary logic operation : NOT, AND, OR, NAND, NOR, etc..
Boole’s binary algebra is used as a formal / mathematical tool to
describe and design complex binary logic circuits.
A logic gate performs a logical operation on one or more logic inputs and produces a single logic output. The logic normally performed is Boolean logic and is most commonly found in digital circuits. Logic gates are primarily implemented electronically using diodes or transistors, but can also be constructed using electromagnetic relays, fluidics, optics, molecules, or even mechanical elements.
In electronic logic, a logic level is represented by a voltage or current, (which depends on the type of electronic logic in use). Each logic gate requires power so that it can source and sink currents to achieve the correct output voltage. In logic circuit diagrams the power is not shown, but in a full electronic schematic, power connections are required.
| Type | Distinctive shape | Rectangular shape | Boolean algebra between A & B | Truth table | ||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | 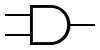 |  |  |
| ||||||||||||||||||
| OR | 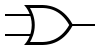 | 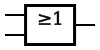 | A + B |
| ||||||||||||||||||
| NOT | 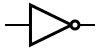 | 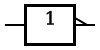 |  |
| ||||||||||||||||||
| In electronics a NOT gate is more commonly called an inverter. The circle on the symbol is called a bubble, and is generally used in circuit diagrams to indicate an inverted (active-low) input or output.[1] | ||||||||||||||||||||||
| NAND |  |  | 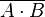 |
| ||||||||||||||||||
| NOR |  |  |  |
| ||||||||||||||||||
| XOR | 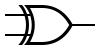 |  | 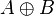 |
| ||||||||||||||||||
| XNOR | 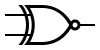 |  |  |
| ||||||||||||||||||
KARNAUGH MAP METHOD
The Karnaugh map (K-map for short), Maurice Karnaugh's 1953 refinement of Edward Veitch's 1952 Veitch diagram, is a method to simplify Boolean algebra expressions. The Karnaugh map reduces the need for extensive calculations by taking advantage of humans' pattern-recognition capability, permitting the rapid identification and elimination of potential race hazards.
In a Karnaugh map the boolean variables are transferred (generally from a truth table) and ordered according to the principles of Gray code in which only one variable changes in between squares. Once the table is generated and the output possibilities are transcribed, the data is arranged into the largest possible groups containing 2n cells (n=0,1,2,3...) and the minterm is generated through the axiom laws of boolean algebra.
Size of map
The size of the Karnaugh map with n Boolean variables is determined by 2n. The size of the group within a Karnaugh map with n Boolean variables and k number of terms in the resulting Boolean expression is determined by 2nk. Common sized maps are of 2 variables which is a 2×2 map, 3 variables which is a 2×4 map, and 4 variables which is a 4×4 map.
Rules of Simplification
The Karnaugh map uses the following rules for the simplification of expressions by grouping together adjacent cells containing ones
- Groups may not include any cell containing a zero

- Groups may be horizontal or vertical, but not diagonal.

- Groups must contain 1, 2, 4, 8, or in general 2n cells.
That is if n = 1, a group will contain two 1's since 21 = 2.
If n = 2, a group will contain four 1's since 22 = 4.
- Each group should be as large as possible.

- Each cell containing a one must be in at least one group.

- Groups may overlap.

- Groups may wrap around the table. The leftmost cell in a row may be grouped with the rightmost cell and the top cell in a column may be grouped with the bottom cell.

- There should be as few groups as possible, as long as this does not contradict any of the previous rules.

Summmary:
- No zeros allowed.
- No diagonals.
- Only power of 2 number of cells in each group.
- Groups should be as large as possible.
- Every one must be in at least one group.
- Overlapping allowed.
- Wrap around allowed.
- Fewest number of groups possible.



No comments:
Post a Comment