Read-Only Memory (ROM)
One major type of memory that is used in PCs is called read-only memory, or ROM for short. ROM is a type of memory that normally can only be read, as opposed to RAM which can be both read and written. There are two main reasons that read-only memory is used for certain functions within the PC:
- Permanence: The values stored in ROM are always there, whether the power is on or not. A ROM can be removed from the PC, stored for an indefinite period of time, and then replaced, and the data it contains will still be there. For this reason, it is called non-volatile storage. A hard disk is also non-volatile, for the same reason, but regular RAM is not.
- Security: The fact that ROM cannot easily be modified provides a measure of security against accidental (or malicious) changes to its contents. You are not going to find viruses infecting true ROMs, for example; it's just not possible. (It's technically possible with erasable EPROMs, though in practice never seen.)
Read-only memory is most commonly used to store system-level programs that we want to have available to the PC at all times. The most common example is the system BIOS program, which is stored in a ROM called (amazingly enough) the system BIOS ROM. Having this in a permanent ROM means it is available when the power is turned on so that the PC can use it to boot up the system. Remember that when you first turn on the PC the system memory is empty, so there has to be something for the PC to use when it starts up.
While the whole point of a ROM is supposed to be that the contents cannot be changed, there are times when being able to change the contents of a ROM can be very useful. There are several ROM variants that can be changed under certain circumstances; these can be thought of as "mostly read-only memory". :^) The following are the different types of ROMs with a description of their relative modifiability:
- ROM: A regular ROM is constructed from hard-wired logic, encoded in the silicon itself, much the way that a processor is. It is designed to perform a specific function and cannot be changed. This is inflexible and so regular ROMs are only used generally for programs that are static (not changing often) and mass-produced. This product is analagous to a commercial software CD-ROM that you purchase in a store.
- Programmable ROM (PROM): This is a type of ROM that can be programmed using special equipment; it can be written to, but only once. This is useful for companies that make their own ROMs from software they write, because when they change their code they can create new PROMs without requiring expensive equipment. This is similar to the way a CD-ROM recorder works by letting you "burn" programs onto blanks once and then letting you read from them many times. In fact, programming a PROM is also called burning, just like burning a CD-R, and it is comparable in terms of its flexibility.
- Erasable Programmable ROM (EPROM): An EPROM is a ROM that can be erased and reprogrammed. A little glass window is installed in the top of the ROM package, through which you can actually see the chip that holds the memory. Ultraviolet light of a specific frequency can be shined through this window for a specified period of time, which will erase the EPROM and allow it to be reprogrammed again. Obviously this is much more useful than a regular PROM, but it does require the erasing light. Continuing the "CD" analogy, this technology is analogous to a reusable CD-RW.
- Electrically Erasable Programmable ROM (EEPROM): The next level of erasability is the EEPROM, which can be erased under software control. This is the most flexible type of ROM, and is now commonly used for holding BIOS programs. When you hear reference to a "flash BIOS" or doing a BIOS upgrade by "flashing", this refers to reprogramming the BIOS EEPROM with a special software program. Here we are blurring the line a bit between what "read-only" really means, but remember that this rewriting is done maybe once a year or so, compared to real read-write memory (RAM) where rewriting is done often many times per second!
Note: One thing that sometimes confuses people is that since RAM is the "opposite" of ROM (since RAM is read-write and ROM is read-only), and since RAM stands for "random access memory", they think that ROM is not random access. This is not true; any location can be read from ROM in any order, so it is random access as well, just not writeable. RAM gets its name because earlier read-write memories were sequential, and did not allow random access.
Finally, one other characteristic of ROM, compared to RAM, is that it is much slower, typically having double the access time of RAM or more.
Random Access Memory (RAM)
The kind of memory used for holding programs and data being executed is called random access memory or RAM. RAM differs from read-only memory (ROM) in that it can be both read and written. It is considered volatile storage because unlike ROM, the contents of RAM are lost when the power is turned off. RAM is also sometimes called read-write memory or RWM. This is actually a much more precise name, so of course it is hardly ever used. :^) It's a better name because calling RAM "random access" implies to some people that ROM isn't random access, which is not true. RAM is called "random access" because earlier read-write memories were sequential and did not allow random access. Sometimes old acronyms persist even when they don't make much sense any more (e.g., the "AT" in the old IBM AT stands for "advanced technology" :^) ).
Obviously, RAM needs to be writeable in order for it to do its job of holding programs and data that you are working on. The volatility of RAM also means that you risk losing what you are working on unless you save it frequently.
RAM is much faster than ROM is, due to the nature of how it stores information. This is why RAM is often used to shadow the BIOS ROM to improve performance when executing BIOS code. There are many different types of RAMs, including static RAM (SRAM) and many flavors of dynamic RAM (DRAM).
Static RAM (SRAM)
Static RAM is a type of RAM that holds its data without external refresh, for as long as power is supplied to the circuit. This is contrasted to dynamic RAM (DRAM), which must be refreshed many times per second in order to hold its data contents. SRAMs are used for specific applications within the PC, where their strengths outweigh their weaknesses compared to DRAM:
- Simplicity: SRAMs don't require external refresh circuitry or other work in order for them to keep their data intact.
- Speed: SRAM is faster than DRAM.
In contrast, SRAMs have the following weaknesses, compared to DRAMs:
- Cost: SRAM is, byte for byte, several times more expensive than DRAM.
- Size: SRAMs take up much more space than DRAMs (which is part of why the cost is higher).
These advantages and disadvantages taken together obviously show that performance-wise, SRAM is superior to DRAM, and we would use it exclusively if only we could do so economically. Unfortunately, 32 MB of SRAM would be prohibitively large and costly, which is why DRAM is used for system memory. SRAMs are used instead for level 1 cache and level 2 cache memory, for which it is perfectly suited; cache memory needs to be very fast, and not very large.
SRAM is manufactured in a way rather similar to how processors are: highly-integrated transistor patterns photo-etched into silicon. Each SRAM bit is comprised of between four and six transistors, which is why SRAM takes up much more space compared to DRAM, which uses only one (plus a capacitor). Because an SRAM chip is comprised of thousands or millions of identical cells, it is much easier to make than a CPU, which is a large die with a non-repetitive structure. This is one reason why RAM chips cost much less than processors do.
Dynamic RAM (DRAM)
Dynamic RAM is a type of RAM that only holds its data if it is continuously accessed by special logic called a refresh circuit. Many hundreds of times each second, this circuitry reads the contents of each memory cell, whether the memory cell is being used at that time by the computer or not. Due to the way in which the cells are constructed, the reading action itself refreshes the contents of the memory. If this is not done regularly, then the DRAM will lose its contents, even if it continues to have power supplied to it. This refreshing action is why the memory is called dynamic.
All PCs use DRAM for their main system memory, instead of SRAM, even though DRAMs are slower than SRAMs and require the overhead of the refresh circuitry. It may seem weird to want to make the computer's memory out of something that can only hold a value for a fraction of a second. In fact, DRAMs are both more complicated and slower than SRAMs.
The reason that DRAMs are used is simple: they are much cheaper and take up much less space, typically 1/4 the silicon area of SRAMs or less. To build a 64 MB core memory from SRAMs would be very expensive. The overhead of the refresh circuit is tolerated in order to allow the use of large amounts of inexpensive, compact memory. The refresh circuitry itself is almost never a problem; many years of using DRAM has caused the design of these circuits to be all but perfected.
DRAMs are smaller and less expensive than SRAMs because SRAMs are made from four to six transistors (or more) per bit, DRAMs use only one, plus a capacitor. The capacitor, when energized, holds an electrical charge if the bit contains a "1" or no charge if it contains a "0". The transistor is used to read the contents of the capacitor. The problem with capacitors is that they only hold a charge for a short period of time, and then it fades away. These capacitors are tiny, so their charges fade particularly quickly. This is why the refresh circuitry is needed: to read the contents of every cell and refresh them with a fresh "charge" before the contents fade away and are lost. Refreshing is done by reading every "row" in the memory chip one row at a time; the process of reading the contents of each capacitor re-establishes the charge.
DRAM is manufactured using a similar process to how processors are: a silicon substrate is etched with the patterns that make the transistors and capacitors (and support structures) that comprise each bit. DRAM costs much less than a processor because it is a series of simple, repeated structures, so there isn't the complexity of making a single chip with several million individually-located transistors. See here for details on how processors are manufactured; the principles for DRAM manufacture are similar.
There are many different kinds of specific DRAM technologies and speeds that they are available in.
FLASH MEMORY
We store and transfer all kinds of files on our computers -- digital photographs, music files, word processing documents, PDFs and countless other forms of media. But sometimes your computer's hard drive isn't exactly where you want your information. Whether you want to make backup copies of files that live off of your systems or if you worry about your security, portable storage devices that use a type of electronic memory called flash memory may be the right solution.
Electronic memory comes in a variety of forms to serve a variety of purposes. Flash memory is used for easy and fast information storage in computers, digital cameras and home video game consoles. It is used more like a hard drive than as RAM. In fact, flash memory is known as a solid state storage device, meaning there are no moving parts -- everything is electronic instead of mechanical.
- Your computer's BIOS chip
- CompactFlash (most often found in digital cameras)
- SmartMedia (most often found in digital cameras)
- Memory Stick (most often found in digital cameras)
- PCMCIA Type I and Type II memory cards (used as solid-state disks in laptops)
- Memory cards for video game consoles
INTERFACING WITH THE ANALOG WORLD
Connecting digital circuitry to sensor devices is simple if the sensor devices are inherently digital themselves. Switches, relays, and encoders are easily interfaced with gate circuits due to the on/off nature of their signals. However, when analog devices are involved, interfacing becomes much more complex. What is needed is a way to electronically translate analog signals into digital (binary) quantities, and vice versa. An analog-to-digital converter, or ADC, performs the former task while a digital-to-analog converter, or DAC, performs the latter.
An ADC inputs an analog electrical signal such as voltage or current and outputs a binary number. In block diagram form, it can be represented as such:
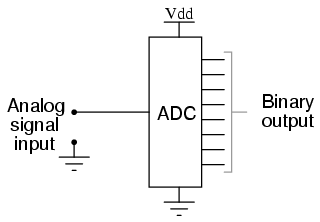
A DAC, on the other hand, inputs a binary number and outputs an analog voltage or current signal. In block diagram form, it looks like this:
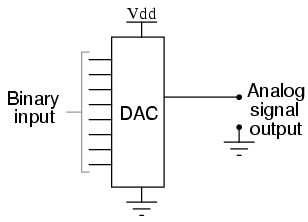
Together, they are often used in digital systems to provide complete interface with analog sensors and output devices for control systems such as those used in automotive engine controls:

It is much easier to convert a digital signal into an analog signal than it is to do the reverse. Therefore, we will begin with DAC circuitry and then move to ADC circuitry.
THE R/2NR ADC
This DAC circuit, otherwise known as the binary-weighted-input DAC, is a variation on the inverting summer op-amp circuit. If you recall, the classic inverting summer circuit is an operational amplifier using negative feedback for controlled gain, with several voltage inputs and one voltage output. The output voltage is the inverted (opposite polarity) sum of all input voltages:

For a simple inverting summer circuit, all resistors must be of equal value. If any of the input resistors were different, the input voltages would have different degrees of effect on the output, and the output voltage would not be a true sum. Let's consider, however, intentionally setting the input resistors at different values. Suppose we were to set the input resistor values at multiple powers of two: R, 2R, and 4R, instead of all the same value R:

Starting from V1 and going through V3, this would give each input voltage exactly half the effect on the output as the voltage before it. In other words, input voltage V1 has a 1:1 effect on the output voltage (gain of 1), while input voltage V2 has half that much effect on the output (a gain of 1/2), and V3 half of that (a gain of 1/4). These ratios are were not arbitrarily chosen: they are the same ratios corresponding to place weights in the binary numeration system. If we drive the inputs of this circuit with digital gates so that each input is either 0 volts or full supply voltage, the output voltage will be an analog representation of the binary value of these three bits.

If we chart the output voltages for all eight combinations of binary bits (000 through 111) input to this circuit, we will get the following progression of voltages:
---------------------------------
| Binary | Output voltage |
---------------------------------
| 000 | 0.00 V |
---------------------------------
| 001 | -1.25 V |
---------------------------------
| 010 | -2.50 V |
---------------------------------
| 011 | -3.75 V |
---------------------------------
| 100 | -5.00 V |
---------------------------------
| 101 | -6.25 V |
---------------------------------
| 110 | -7.50 V |
---------------------------------
| 111 | -8.75 V |
---------------------------------
Note that with each step in the binary count sequence, there results a 1.25 volt change in the output. This circuit is very easy to simulate using SPICE. In the following simulation, I set up the DAC circuit with a binary input of 110 (note the first node numbers for resistors R1, R2, and R3: a node number of "1" connects it to the positive side of a 5 volt battery, and a node number of "0" connects it to ground). The output voltage appears on node 6 in the simulation:

binary-weighted dac
v1 1 0 dc 5
rbogus 1 0 99k
r1 1 5 1k
r2 1 5 2k
r3 0 5 4k
rfeedbk 5 6 1k
e1 6 0 5 0 999k
.end
node voltage node voltage node voltage
(1) 5.0000 (5) 0.0000 (6) -7.5000
We can adjust resistors values in this circuit to obtain output voltages directly corresponding to the binary input. For example, by making the feedback resistor 800 Ω instead of 1 kΩ, the DAC will output -1 volt for the binary input 001, -4 volts for the binary input 100, -7 volts for the binary input 111, and so on.
(with feedback resistor set at 800 ohms)
---------------------------------
| Binary | Output voltage |
---------------------------------
| 000 | 0.00 V |
---------------------------------
| 001 | -1.00 V |
---------------------------------
| 010 | -2.00 V |
---------------------------------
| 011 | -3.00 V |
---------------------------------
| 100 | -4.00 V |
---------------------------------
| 101 | -5.00 V |
---------------------------------
| 110 | -6.00 V |
---------------------------------
| 111 | -7.00 V |
---------------------------------
If we wish to expand the resolution of this DAC (add more bits to the input), all we need to do is add more input resistors, holding to the same power-of-two sequence of values:

It should be noted that all logic gates must output exactly the same voltages when in the "high" state. If one gate is outputting +5.02 volts for a "high" while another is outputting only +4.86 volts, the analog output of the DAC will be adversely affected. Likewise, all "low" voltage levels should be identical between gates, ideally 0.00 volts exactly. It is recommended that CMOS output gates are used, and that input/feedback resistor values are chosen so as to minimize the amount of current each gate has to source or sink.
THE R/2R DAC
An alternative to the binary-weighted-input DAC is the so-called R/2R DAC, which uses fewer unique resistor values. A disadvantage of the former DAC design was its requirement of several different precise input resistor values: one unique value per binary input bit. Manufacture may be simplified if there are fewer different resistor values to purchase, stock, and sort prior to assembly.
Of course, we could take our last DAC circuit and modify it to use a single input resistance value, by connecting multiple resistors together in series:

Unfortunately, this approach merely substitutes one type of complexity for another: volume of components over diversity of component values. There is, however, a more efficient design methodology.
By constructing a different kind of resistor network on the input of our summing circuit, we can achieve the same kind of binary weighting with only two kinds of resistor values, and with only a modest increase in resistor count. This "ladder" network looks like this:

Mathematically analyzing this ladder network is a bit more complex than for the previous circuit, where each input resistor provided an easily-calculated gain for that bit. For those who are interested in pursuing the intricacies of this circuit further, you may opt to use Thevenin's theorem for each binary input (remember to consider the effects of the virtual ground), and/or use a simulation program like SPICE to determine circuit response. Either way, you should obtain the following table of figures:
---------------------------------
| Binary | Output voltage |
---------------------------------
| 000 | 0.00 V |
---------------------------------
| 001 | -1.25 V |
---------------------------------
| 010 | -2.50 V |
---------------------------------
| 011 | -3.75 V |
---------------------------------
| 100 | -5.00 V |
---------------------------------
| 101 | -6.25 V |
---------------------------------
| 110 | -7.50 V |
---------------------------------
| 111 | -8.75 V |
---------------------------------
As was the case with the binary-weighted DAC design, we can modify the value of the feedback resistor to obtain any "span" desired. For example, if we're using +5 volts for a "high" voltage level and 0 volts for a "low" voltage level, we can obtain an analog output directly corresponding to the binary input (011 = -3 volts, 101 = -5 volts, 111 = -7 volts, etc.) by using a feedback resistance with a value of 1.6R instead of 2R.
FLASH ADC
Also called the parallel A/D converter, this circuit is the simplest to understand. It is formed of a series of comparators, each one comparing the input signal to a unique reference voltage. The comparator outputs connect to the inputs of a priority encoder circuit, which then produces a binary output. The following illustration shows a 3-bit flash ADC circuit:
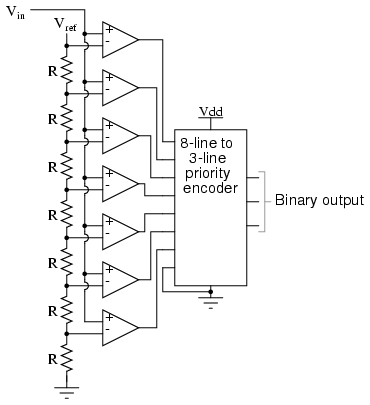
Vref is a stable reference voltage provided by a precision voltage regulator as part of the converter circuit, not shown in the schematic. As the analog input voltage exceeds the reference voltage at each comparator, the comparator outputs will sequentially saturate to a high state. The priority encoder generates a binary number based on the highest-order active input, ignoring all other active inputs.
When operated, the flash ADC produces an output that looks something like this:

For this particular application, a regular priority encoder with all its inherent complexity isn't necessary. Due to the nature of the sequential comparator output states (each comparator saturating "high" in sequence from lowest to highest), the same "highest-order-input selection" effect may be realized through a set of Exclusive-OR gates, allowing the use of a simpler, non-priority encoder:

And, of course, the encoder circuit itself can be made from a matrix of diodes, demonstrating just how simply this converter design may be constructed:
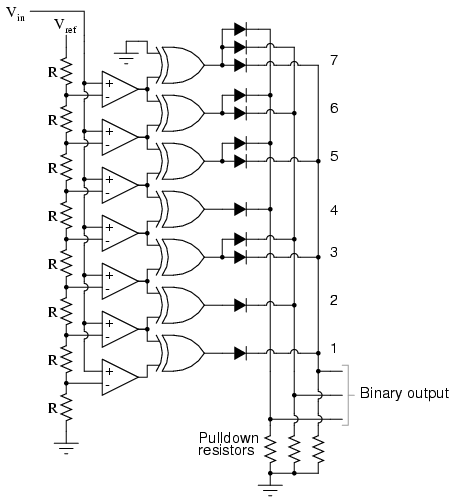
Not only is the flash converter the simplest in terms of operational theory, but it is the most efficient of the ADC technologies in terms of speed, being limited only in comparator and gate propagation delays. Unfortunately, it is the most component-intensive for any given number of output bits. This three-bit flash ADC requires seven comparators. A four-bit version would require 15 comparators. With each additional output bit, the number of required comparators doubles. Considering that eight bits is generally considered the minimum necessary for any practical ADC (255 comparators needed!), the flash methodology quickly shows its weakness.
An additional advantage of the flash converter, often overlooked, is the ability for it to produce a non-linear output. With equal-value resistors in the reference voltage divider network, each successive binary count represents the same amount of analog signal increase, providing a proportional response. For special applications, however, the resistor values in the divider network may be made non-equal. This gives the ADC a custom, nonlinear response to the analog input signal. No other ADC design is able to grant this signal-conditioning behavior with just a few component value changes.
DIGITAL RAMP ADC
Also known as the stairstep-ramp, or simply counter A/D converter, this is also fairly easy to understand but unfortunately suffers from several limitations.
The basic idea is to connect the output of a free-running binary counter to the input of a DAC, then compare the analog output of the DAC with the analog input signal to be digitized and use the comparator's output to tell the counter when to stop counting and reset. The following schematic shows the basic idea:

As the counter counts up with each clock pulse, the DAC outputs a slightly higher (more positive) voltage. This voltage is compared against the input voltage by the comparator. If the input voltage is greater than the DAC output, the comparator's output will be high and the counter will continue counting normally. Eventually, though, the DAC output will exceed the input voltage, causing the comparator's output to go low. This will cause two things to happen: first, the high-to-low transition of the comparator's output will cause the shift register to "load" whatever binary count is being output by the counter, thus updating the ADC circuit's output; secondly, the counter will receive a low signal on the active-low LOAD input, causing it to reset to 00000000 on the next clock pulse.
The effect of this circuit is to produce a DAC output that ramps up to whatever level the analog input signal is at, output the binary number corresponding to that level, and start over again. Plotted over time, it looks like this:

Note how the time between updates (new digital output values) changes depending on how high the input voltage is. For low signal levels, the updates are rather close-spaced. For higher signal levels, they are spaced further apart in time:

For many ADC applications, this variation in update frequency (sample time) would not be acceptable. This, and the fact that the circuit's need to count all the way from 0 at the beginning of each count cycle makes for relatively slow sampling of the analog signal, places the digital-ramp ADC at a disadvantage to other counter strategies.
SUCCESSIVE APPROXIMATION ADC
One method of addressing the digital ramp ADC's shortcomings is the so-called successive-approximation ADC. The only change in this design is a very special counter circuit known as a successive-approximation register. Instead of counting up in binary sequence, this register counts by trying all values of bits starting with the most-significant bit and finishing at the least-significant bit. Throughout the count process, the register monitors the comparator's output to see if the binary count is less than or greater than the analog signal input, adjusting the bit values accordingly. The way the register counts is identical to the "trial-and-fit" method of decimal-to-binary conversion, whereby different values of bits are tried from MSB to LSB to get a binary number that equals the original decimal number. The advantage to this counting strategy is much faster results: the DAC output converges on the analog signal input in much larger steps than with the 0-to-full count sequence of a regular counter.
Without showing the inner workings of the successive-approximation register (SAR), the circuit looks like this:

It should be noted that the SAR is generally capable of outputting the binary number in serial (one bit at a time) format, thus eliminating the need for a shift register. Plotted over time, the operation of a successive-approximation ADC looks like this:

Note how the updates for this ADC occur at regular intervals, unlike the digital ramp ADC circuit.
TRACKING ADC
A third variation on the counter-DAC-based converter theme is, in my estimation, the most elegant. Instead of a regular "up" counter driving the DAC, this circuit uses an up/down counter. The counter is continuously clocked, and the up/down control line is driven by the output of the comparator. So, when the analog input signal exceeds the DAC output, the counter goes into the "count up" mode. When the DAC output exceeds the analog input, the counter switches into the "count down" mode. Either way, the DAC output always counts in the proper direction to track the input signal.

Notice how no shift register is needed to buffer the binary count at the end of a cycle. Since the counter's output continuously tracks the input (rather than counting to meet the input and then resetting back to zero), the binary output is legitimately updated with every clock pulse.
An advantage of this converter circuit is speed, since the counter never has to reset. Note the behavior of this circuit:

Note the much faster update time than any of the other "counting" ADC circuits. Also note how at the very beginning of the plot where the counter had to "catch up" with the analog signal, the rate of change for the output was identical to that of the first counting ADC. Also, with no shift register in this circuit, the binary output would actually ramp up rather than jump from zero to an accurate count as it did with the counter and successive approximation ADC circuits.
Perhaps the greatest drawback to this ADC design is the fact that the binary output is never stable: it always switches between counts with every clock pulse, even with a perfectly stable analog input signal. This phenomenon is informally known as bit bobble, and it can be problematic in some digital systems.
This tendency can be overcome, though, through the creative use of a shift register. For example, the counter's output may be latched through a parallel-in/parallel-out shift register only when the output changes by two or more steps. Building a circuit to detect two or more successive counts in the same direction takes a little ingenuity, but is worth the effort.
DIGITAL VOLTMETER
The first digital voltmeter was invented and produced by Andrew Kay of Non-Linear Systems (and later founder of Kaypro) in 1954.
Digital voltmeters (DVMs) are usually designed around a special type of analog-to-digital converter called an integrating converter.
Voltmeter accuracy is affected by many factors, including temperature and supply voltage variations. To ensure that a digital voltmeter's reading is within the manufacturer's specified tolerances, they should be periodically calibrated against a voltage standard such as the Weston cell.
Digital voltmeters necessarily have input amplifiers, and, like vacuum tube voltmeters, generally have a constant input resistance of 10 megohms regardless of set measurement range.
No comments:
Post a Comment