DIGITAL ARITHMETIC: OPERATIONS AND CIRCUITS

BINARY ADDITION

Adding binary numbers is a very simple task, and very similar to the longhand addition of decimal numbers. As with decimal numbers, you start by adding the bits (digits) one column, or place weight, at a time, from right to left. Unlike decimal addition, there is little to memorize in the way of rules for the addition of binary bits:

0 + 0 = 0
1 + 0 = 1
0 + 1 = 1
1 + 1 = 10
1 + 1 + 1 = 11

Just as with decimal addition, when the sum in one column is a two-bit (two-digit) number, the least significant figure is written as part of the total sum and the most significant figure is "carried" to the next left column. Consider the following examples:

.                          11  1 <--- Carry bits ----->  11
.     1001101             1001001                     1000111
.   + 0010010           + 0011001                   + 0010110
.   ---------           ---------                   ---------
.     1011111             1100010                     1011101

The addition problem on the left did not require any bits to be carried, since the sum of bits in each column was either 1 or 0, not 10 or 11. In the other two problems, there definitely were bits to be carried, but the process of addition is still quite simple.

As we'll see later, there are ways that electronic circuits can be built to perform this very task of addition, by representing each bit of each binary number as a voltage signal (either "high," for a 1; or "low" for a 0). This is the very foundation of all the arithmetic which modern digital computers perform.

NEGATIVE BINARY NUMBERS

With addition being easily accomplished, we can perform the operation of subtraction with the same technique simply by making one of the numbers negative. For example, the subtraction problem of 7 - 5 is essentially the same as the addition problem 7 + (-5). Since we already know how to represent positive numbers in binary, all we need to know now is how to represent their negative counterparts and we'll be able to subtract.

Usually we represent a negative decimal number by placing a minus sign directly to the left of the most significant digit, just as in the example above, with -5. However, the whole purpose of using binary notation is for constructing on/off circuits that can represent bit values in terms of voltage (2 alternative values: either "high" or "low"). In this context, we don't have the luxury of a third symbol such as a "minus" sign, since these circuits can only be on or off (two possible states). One solution is to reserve a bit (circuit) that does nothing but represent the mathematical sign:

.                        1012 = 510    (positive)
.
.  Extra bit, representing sign (0=positive, 1=negative)
.                       |
.                       01012 = 510    (positive)
.
.  Extra bit, representing sign (0=positive, 1=negative)
.                       |
.                       11012 = -510   (negative)

As you can see, we have to be careful when we start using bits for any purpose other than standard place-weighted values. Otherwise, 1101₂ could be misinterpreted as the number thirteen when in fact we mean to represent negative five. To keep things straight here, we must first decide how many bits are going to be needed to represent the largest numbers we'll be dealing with, and then be sure not to exceed that bit field length in our arithmetic operations. For the above example, I've limited myself to the representation of numbers from negative seven (1111₂) to positive seven (0111₂), and no more, by making the fourth bit the "sign" bit. Only by first establishing these limits can I avoid confusion of a negative number with a larger, positive number.

Representing negative five as 1101₂ is an example of the sign-magnitude system of negative binary numeration. By using the leftmost bit as a sign indicator and not a place-weighted value, I am sacrificing the "pure" form of binary notation for something that gives me a practical advantage: the representation of negative numbers. The leftmost bit is read as the sign, either positive or negative, and the remaining bits are interpreted according to the standard binary notation: left to right, place weights in multiples of two.

As simple as the sign-magnitude approach is, it is not very practical for arithmetic purposes. For instance, how do I add a negative five (1101₂) to any other number, using the standard technique for binary addition? I'd have to invent a new way of doing addition in order for it to work, and if I do that, I might as well just do the job with longhand subtraction; there's no arithmetical advantage to using negative numbers to perform subtraction through addition if we have to do it with sign-magnitude numeration, and that was our goal!

There's another method for representing negative numbers which works with our familiar technique of longhand addition, and also happens to make more sense from a place-weighted numeration point of view, called complementation. With this strategy, we assign the leftmost bit to serve a special purpose, just as we did with the sign-magnitude approach, defining our number limits just as before. However, this time, the leftmost bit is more than just a sign bit; rather, it possesses a negative place-weight value. For example, a value of negative five would be represented as such:

Extra bit, place weight = negative eight
.                    |
.                    10112 = 510   (negative)
.
.          (1 x -810)  +  (0 x 410)  +  (1 x 210)  +  (1 x 110)  =  -510

With the right three bits being able to represent a magnitude from zero through seven, and the leftmost bit representing either zero or negative eight, we can successfully represent any integer number from negative seven (1001₂ = -8₁₀ + 1₁₀ = -7₁₀) to positive seven (0111₂ = 0₁₀ + 7₁₀ = 7₁₀).

Representing positive numbers in this scheme (with the fourth bit designated as the negative weight) is no different from that of ordinary binary notation. However, representing negative numbers is not quite as straightforward:

zero             0000
positive one     0001          negative one     1111
positive two     0010          negative two     1110
positive three   0011          negative three   1101
positive four    0100          negative four    1100
positive five    0101          negative five    1011
positive six     0110          negative six     1010
positive seven   0111          negative seven   1001
.                              negative eight   1000

Note that the negative binary numbers in the right column, being the sum of the right three bits' total plus the negative eight of the leftmost bit, don't "count" in the same progression as the positive binary numbers in the left column. Rather, the right three bits have to be set at the proper value to equal the desired (negative) total when summed with the negative eight place value of the leftmost bit.

Those right three bits are referred to as the two's complement of the corresponding positive number. Consider the following comparison:

positive number       two's complement
---------------       ----------------
001                    111
010                    110
011                    101
100                    100
101                    011
110                    010
111                    001

In this case, with the negative weight bit being the fourth bit (place value of negative eight), the two's complement for any positive number will be whatever value is needed to add to negative eight to make that positive value's negative equivalent. Thankfully, there's an easy way to figure out the two's complement for any binary number: simply invert all the bits of that number, changing all 1's to 0's and vice versa (to arrive at what is called the one's complement) and then add one! For example, to obtain the two's complement of five (101₂), we would first invert all the bits to obtain 010₂ (the "one's complement"), then add one to obtain 011₂, or -5₁₀ in three-bit, two's complement form.

Interestingly enough, generating the two's complement of a binary number works the same if you manipulate all the bits, including the leftmost (sign) bit at the same time as the magnitude bits. Let's try this with the former example, converting a positive five to a negative five, but performing the complementation process on all four bits. We must be sure to include the 0 (positive) sign bit on the original number, five (0101₂). First, inverting all bits to obtain the one's complement: 1010₂. Then, adding one, we obtain the final answer: 1011₂, or -5₁₀ expressed in four-bit, two's complement form.

It is critically important to remember that the place of the negative-weight bit must be already determined before any two's complement conversions can be done. If our binary numeration field were such that the eighth bit was designated as the negative-weight bit (10000000₂), we'd have to determine the two's complement based on all seven of the other bits. Here, the two's complement of five (0000101₂) would be 1111011₂. A positive five in this system would be represented as 00000101₂, and a negative five as 11111011₂.

BINARY SUBTRACTION

We can subtract one binary number from another by using the standard techniques adapted for decimal numbers (subtraction of each bit pair, right to left, "borrowing" as needed from bits to the left). However, if we can leverage the already familiar (and easier) technique of binary addition to subtract, that would be better. As we just learned, we can represent negative binary numbers by using the "two's complement" method and a negative place-weight bit. Here, we'll use those negative binary numbers to subtract through addition. Here's a sample problem:

Subtraction: 710 - 510         Addition equivalent:  710 + (-510)

If all we need to do is represent seven and negative five in binary (two's complemented) form, all we need is three bits plus the negative-weight bit:

positive seven = 01112
negative five  = 10112

Now, let's add them together:

.                    1111  <--- Carry bits .                     0111 .                   + 1011 .                   ------ .                    10010 .                    | .             Discard extra bit . .            Answer = 00102

Since we've already defined our number bit field as three bits plus the negative-weight bit, the fifth bit in the answer (1) will be discarded to give us a result of 0010₂, or positive two, which is the correct answer.

Another way to understand why we discard that extra bit is to remember that the leftmost bit of the lower number possesses a negative weight, in this case equal to negative eight. When we add these two binary numbers together, what we're actually doing with the MSBs is subtracting the lower number's MSB from the upper number's MSB. In subtraction, one never "carries" a digit or bit on to the next left place-weight.

Let's try another example, this time with larger numbers. If we want to add -25₁₀ to 18₁₀, we must first decide how large our binary bit field must be. To represent the largest (absolute value) number in our problem, which is twenty-five, we need at least five bits, plus a sixth bit for the negative-weight bit. Let's start by representing positive twenty-five, then finding the two's complement and putting it all together into one numeration:

+2510  = 0110012 (showing all six bits)
One's complement of 110012 = 1001102
One's complement + 1 = two's complement = 1001112 
-2510 = 1001112

Essentially, we're representing negative twenty-five by using the negative-weight (sixth) bit with a value of negative thirty-two, plus positive seven (binary 111₂).

Now, let's represent positive eighteen in binary form, showing all six bits:

.              1810  = 0100102
.
.       Now, let's add them together and see what we get:
.
.                     11   <--- Carry bits .                   100111 .                 + 010010 .                 -------- .                   111001 

Since there were no "extra" bits on the left, there are no bits to discard. The leftmost bit on the answer is a 1, which means that the answer is negative, in two's complement form, as it should be. Converting the answer to decimal form by summing all the bits times their respective weight values, we get:

(1 x -3210)  +  (1 x 1610)  +  (1 x 810)  +  (1 x 110)  = -710

Indeed -7₁₀ is the proper sum of -25₁₀ and 18₁₀.

2's COMPLEMENT SYSTEM

Property

Two's complement representation allows the use of binary arithmetic operations on signed integers, yielding the correct 2's complement results.

Positive Numbers

Positive 2's complement numbers are represented as the simple binary.

Negative Numbers

Negative 2's complement numbers are represented as the binary number that when added to a positive number of the same magnitude equals zero.

Integer		2's Complement
Signed	Unsigned
5	5	0000 0101
4	4	0000 0100
3	3	0000 0011
2	2	0000 0010
1	1	0000 0001
0	0	0000 0000
-1	255	1111 1111
-2	254	1111 1110
-3	253	1111 1101
-4	252	1111 1100
-5	251	1111 1011

Note: The most significant (leftmost) bit indicates the sign of the integer; therefore it is sometimes called the sign bit.

If the sign bit is zero,

then the number is greater than or equal to zero, or positive.

If the sign bit is one,

then the number is less than zero, or negative.

Calculation of 2's Complement

To calculate the 2's complement of an integer, invert the binary equivalent of the number by changing all of the ones to zeroes and all of the zeroes to ones (also called 1's complement), and then add one.

For example,

0001 0001(binary 17) 1110 1111(two's complement -17)
NOT(0001 0001)	=	1110 1110 (Invert bits)
1110 1110 + 0000 0001	=	1110 1111 (Add 1)

2's Complement Addition

Two's complement addition follows the same rules as binary addition.

For example,

5 + (-3) = 2		0000 0101	=	+5
		+ 1111 1101	=	-3
		0000 0010	=	+2

2's Complement Subtraction

Two's complement subtraction is the binary addition of the minuend to the 2's complement of the subtrahend (adding a negative number is the same as subtracting a positive one).

For example,

7 - 12 = (-5)		0000 0111	=	+7
		+ 1111 0100	=	-12
		1111 1011	=	-5

2's Complement Multiplication

Two's complement multiplication follows the same rules as binary multiplication.

For example,

(-4) × 4 = (-16)		1111 1100	=	-4
		× 0000 0100	=	+4
		1111 0000	=	-16

2's Complement Division

Two's complement division is repeated 2's complement subtraction. The 2's complement of the divisor is calculated, then added to the dividend. For the next subtraction cycle, the quotient replaces the dividend. This repeats until the quotient is too small for subtraction or is zero, then it becomes the remainder. The final answer is the total of subtraction cycles plus the remainder.

For example,

7 ÷ 3 = 2 remainder 1		0000 0111	=	+7		0000 0100	=	+4
		+ 1111 1101	=	-3		+ 1111 1101	=	-3
		0000 0100	=	+4		0000 0001	=	+1 (remainder)

Sign Extension

To extend a signed integer from 8 bits to 16 bits or from 16 bits to 32 bits, append additional bits on the left side of the number. Fill each extra bit with the value of the smaller number's most significant bit (the sign bit).

For example,

Signed Integer	8-bit Representation	16-bit Representation
-1	1111 1111	1111 1111 1111 1111
+1	0000 0001	0000 0000 0000 0001

Other Representations of Signed Integers

Sign-Magnitude Representation

Another method of representing negative numbers is sign-magnitude. Sign-magnitude representation also uses the most significant bit of the number to indicate the sign. A negative number is the 7-bit binary representation of the positive number with the most significant bit set to one. The drawbacks to using this method for arithmetic computation are that a different set of rules are required and that zero can have two representations (+0, 0000 0000 and -0, 1000 0000).

Offset Binary Representation

A third method for representing signed numbers is offset binary. Begin calculating a offset binary code by assigning half of the largest possible number as the zero value. A positive integer is the absolute value added to the zero number and a negative integer is subtracted. Offset binary is popular in A/D and D/A conversions, but it is still awkward for arithmetic computation.

For example,

Largest value for 8-bit integer = 28 = 256

Offset binary zero value = 256 ÷ 2 = 128(decimal) = 1000 0000(binary)

1000 0000(offset binary 0) + 0001 0110(binary 22) = 1001 0110(offset binary +22)

1000 0000(offset binary 0) - 0000 0111(binary 7) = 0111 1001(offset binary -7)

Signed Integer	Sign Magnitude	Offset Binary
+5	0000 0101	1000 0101
+4	0000 0100	1000 0100
+3	0000 0011	1000 0011
+2	0000 0010	1000 0010
+1	0000 0001	1000 0001
0	0000 0000 1000 0000	1000 0000
-1	1000 0001	0111 1111
-2	1000 0010	0111 1110
-3	1000 0011	0111 1101
-4	1000 0100	0111 1100
-5	1000 0101	0111 1011

ARITHMETIC CIRCUITS



Arithmetic circuits are the ones which perform arithmetic operations like addition, subtraction, multiplication, division, parity calculation. Most of the time, designing these circuits is the same as designing muxers, encoders and decoders.


ADDERS



Adders are the basic building blocks of all arithmetic circuits; adders add two binary numbers and give out sum and carry as output. Basically we have two types of adders.

• Half Adder
• Full Adder

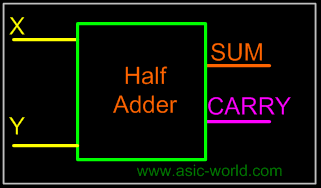
Half Adder


Adding two single-bit binary values X, Y produces a sum S bit and a carry out C-out bit. This operation is called half addition and the circuit to realize it is called a half adder.

Truth Table

		X Y SUM CARRY 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1

	Symbol
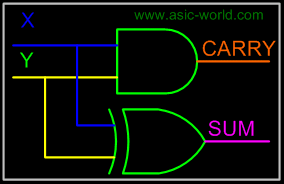
		S (X,Y) = (1,2)
		S = X'Y + XY'
		S = XY
		CARRY(X,Y) = (3)
		CARRY = XY

Circuit

Full Adder

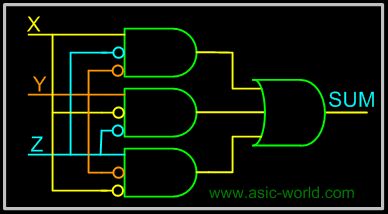
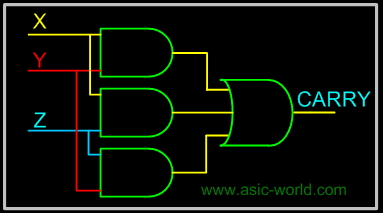
	The below implementation shows implementing the full adder with AND-OR gates, instead of using XOR gates. The basis of the circuit below is from the above Kmap.

Circuit-SUM

	Circuit-CARRY

FULL ADDER USING AND-OR

	Circuit-SUM

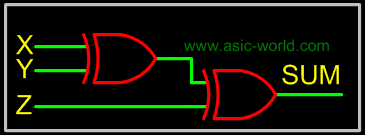	Circuit-CARRY

BCD ADDER



BCD addition is the same as binary addition with a bit of variation: whenever a sum is greater than 1001, it is not a valid BCD number, so we add 0110 to it, to do the correction. This will produce a carry, which is added to the next BCD position.

• Add the two 4-bit BCD code inputs.
• Determine if the sum of this addition is greater than 1001; if yes, then add 0110 to this sum and generate a carry to the next decimal position.

MULTIPLIERS

Multiplication is achieved by adding a list of shifted multiplicands according to the digits of the multiplier. An n-bit X n-bit multiplier can be realized in combinational circuitry by using an array of n-1 n-bit adders where each adder is shifted by one position. For each adder one input is the shifted multiplicand multiplied by 0 or 1 (using AND gates) depending on the multiplier bit, the other input is n partial product bits.

IIEE/ANSI SYMBOLS



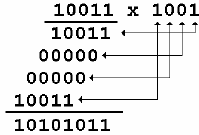
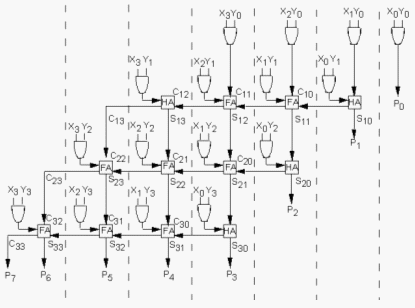
Together with the American National Standards Institute (ANSI), the Institute of ANSI
Electrical and Electronic Engineers (IEEE) has developed a standard set of logic IEEE
symbols. The most recent revision of the standard is ANSI/IEEE Std 91-1984,
IEEE Standard Graphic Symbols for Logic Functions. It is compatible with
standard 617 of the International Electrotechnical Commission (IEC), and must
be used in all logic diagrams drawn for the U.S. Department of Defense.

http://www.ddpp.com/DDPP3_pdf/IEEEsyms.pdf