A circuit with flip-flops is considered a sequential
circuit even in the absence of combinational logic.
Circuits that include flip-flops are usually classified
by the function they perform. Two such circuits are
registers and counters:
> Register – is a group of flip-flops. Its basic
function is to hold information within a digital
system so as to make it available to the logic
units during the computing process. However,
a register may also have additional capabilities
associated with it.
> Counter – is essentially a register that goes
through a predetermined sequence of states.
The gates in the counter are connected in such
a way as to produce the prescribed sequence
of binary states.
Applications of registers include serial addition,
convolutional encoders for error-control coding,
and pseudo-random binary sequence generators.
Counters are primarily used as pattern generators
SYNCHRONOUS COUNTER
A synchronous counter, in contrast to an asynchronous counter, is one whose output bits change state simultaneously, with no ripple. The only way we can build such a counter circuit from J-K flip-flops is to connect all the clock inputs together, so that each and every flip-flop receives the exact same clock pulse at the exact same time:

Now, the question is, what do we do with the J and K inputs? We know that we still have to maintain the same divide-by-two frequency pattern in order to count in a binary sequence, and that this pattern is best achieved utilizing the "toggle" mode of the flip-flop, so the fact that the J and K inputs must both be (at times) "high" is clear. However, if we simply connect all the J and K inputs to the positive rail of the power supply as we did in the asynchronous circuit, this would clearly not work because all the flip-flops would toggle at the same time: with each and every clock pulse!

Let's examine the four-bit binary counting sequence again, and see if there are any other patterns that predict the toggling of a bit. Asynchronous counter circuit design is based on the fact that each bit toggle happens at the same time that the preceding bit toggles from a "high" to a "low" (from 1 to 0). Since we cannot clock the toggling of a bit based on the toggling of a previous bit in a synchronous counter circuit (to do so would create a ripple effect) we must find some other pattern in the counting sequence that can be used to trigger a bit toggle:
Examining the four-bit binary count sequence, another predictive pattern can be seen. Notice that just before a bit toggles, all preceding bits are "high:"

This pattern is also something we can exploit in designing a counter circuit. If we enable each J-K flip-flop to toggle based on whether or not all preceding flip-flop outputs (Q) are "high," we can obtain the same counting sequence as the asynchronous circuit without the ripple effect, since each flip-flop in this circuit will be clocked at exactly the same time:

The result is a four-bit synchronous "up" counter. Each of the higher-order flip-flops are made ready to toggle (both J and K inputs "high") if the Q outputs of all previous flip-flops are "high." Otherwise, the J and K inputs for that flip-flop will both be "low," placing it into the "latch" mode where it will maintain its present output state at the next clock pulse. Since the first (LSB) flip-flop needs to toggle at every clock pulse, its J and K inputs are connected to Vcc or Vdd, where they will be "high" all the time. The next flip-flop need only "recognize" that the first flip-flop's Q output is high to be made ready to toggle, so no AND gate is needed. However, the remaining flip-flops should be made ready to toggle only when all lower-order output bits are "high," thus the need for AND gates.
To make a synchronous "down" counter, we need to build the circuit to recognize the appropriate bit patterns predicting each toggle state while counting down. Not surprisingly, when we examine the four-bit binary count sequence, we see that all preceding bits are "low" prior to a toggle (following the sequence from bottom to top):

Since each J-K flip-flop comes equipped with a Q' output as well as a Q output, we can use the Q' outputs to enable the toggle mode on each succeeding flip-flop, being that each Q' will be "high" every time that the respective Q is "low:"

Taking this idea one step further, we can build a counter circuit with selectable between "up" and "down" count modes by having dual lines of AND gates detecting the appropriate bit conditions for an "up" and a "down" counting sequence, respectively, then use OR gates to combine the AND gate outputs to the J and K inputs of each succeeding flip-flop:
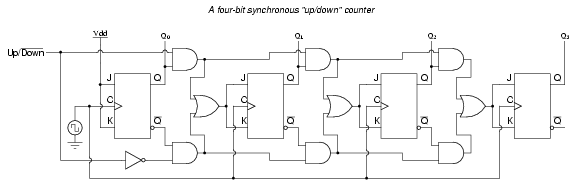
This circuit isn't as complex as it might first appear. The Up/Down control input line simply enables either the upper string or lower string of AND gates to pass the Q/Q' outputs to the succeeding stages of flip-flops. If the Up/Down control line is "high," the top AND gates become enabled, and the circuit functions exactly the same as the first ("up") synchronous counter circuit shown in this section. If the Up/Down control line is made "low," the bottom AND gates become enabled, and the circuit functions identically to the second ("down" counter) circuit shown in this section.
To illustrate, here is a diagram showing the circuit in the "up" counting mode (all disabled circuitry shown in grey rather than black):
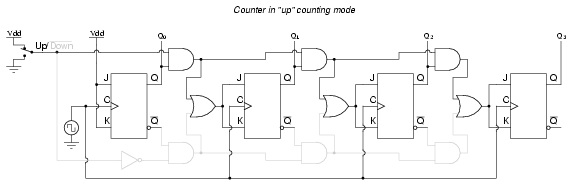
Here, shown in the "down" counting mode, with the same grey coloring representing disabled circuitry:

ASYNCHRONOUS COUNTER
Since we know that binary count sequences follow a pattern of octave (factor of 2) frequency division, and that J-K flip-flop multivibrators set up for the "toggle" mode are capable of performing this type of frequency division, we can envision a circuit made up of several J-K flip-flops, cascaded to produce four bits of output. The main problem facing us is to determine how to connect these flip-flops together so that they toggle at the right times to produce the proper binary sequence. Examine the following binary count sequence, paying attention to patterns preceding the "toggling" of a bit between 0 and 1:

Note that each bit in this four-bit sequence toggles when the bit before it (the bit having a lesser significance, or place-weight), toggles in a particular direction: from 1 to 0. Small arrows indicate those points in the sequence where a bit toggles, the head of the arrow pointing to the previous bit transitioning from a "high" (1) state to a "low" (0) state:

Starting with four J-K flip-flops connected in such a way to always be in the "toggle" mode, we need to determine how to connect the clock inputs in such a way so that each succeeding bit toggles when the bit before it transitions from 1 to 0. The Q outputs of each flip-flop will serve as the respective binary bits of the final, four-bit count:

If we used flip-flops with negative-edge triggering (bubble symbols on the clock inputs), we could simply connect the clock input of each flip-flop to the Q output of the flip-flop before it, so that when the bit before it changes from a 1 to a 0, the "falling edge" of that signal would "clock" the next flip-flop to toggle the next bit:

This circuit would yield the following output waveforms, when "clocked" by a repetitive source of pulses from an oscillator:

The first flip-flop (the one with the Q0 output), has a positive-edge triggered clock input, so it toggles with each rising edge of the clock signal. Notice how the clock signal in this example has a duty cycle less than 50%. I've shown the signal in this manner for the purpose of demonstrating how the clock signal need not be symmetrical to obtain reliable, "clean" output bits in our four-bit binary sequence. In the very first flip-flop circuit shown in this chapter, I used the clock signal itself as one of the output bits. This is a bad practice in counter design, though, because it necessitates the use of a square wave signal with a 50% duty cycle ("high" time = "low" time) in order to obtain a count sequence where each and every step pauses for the same amount of time. Using one J-K flip-flop for each output bit, however, relieves us of the necessity of having a symmetrical clock signal, allowing the use of practically any variety of high/low waveform to increment the count sequence.
As indicated by all the other arrows in the pulse diagram, each succeeding output bit is toggled by the action of the preceding bit transitioning from "high" (1) to "low" (0). This is the pattern necessary to generate an "up" count sequence.
A less obvious solution for generating an "up" sequence using positive-edge triggered flip-flops is to "clock" each flip-flop using the Q' output of the preceding flip-flop rather than the Q output. Since the Q' output will always be the exact opposite state of the Q output on a J-K flip-flop (no invalid states with this type of flip-flop), a high-to-low transition on the Q output will be accompanied by a low-to-high transition on the Q' output. In other words, each time the Q output of a flip-flop transitions from 1 to 0, the Q' output of the same flip-flop will transition from 0 to 1, providing the positive-going clock pulse we would need to toggle a positive-edge triggered flip-flop at the right moment:

One way we could expand the capabilities of either of these two counter circuits is to regard the Q' outputs as another set of four binary bits. If we examine the pulse diagram for such a circuit, we see that the Q' outputs generate a down-counting sequence, while the Q outputs generate an up-counting sequence:
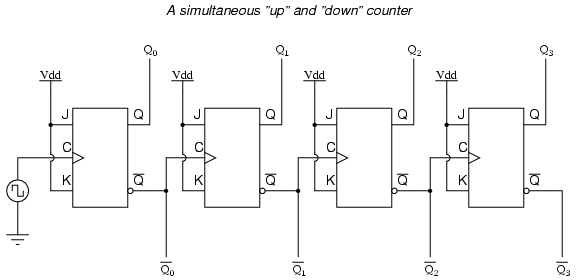

Unfortunately, all of the counter circuits shown thusfar share a common problem: the ripple effect. This effect is seen in certain types of binary adder and data conversion circuits, and is due to accumulative propagation delays between cascaded gates. When the Q output of a flip-flop transitions from 1 to 0, it commands the next flip-flop to toggle. If the next flip-flop toggle is a transition from 1 to 0, it will command the flip-flop after it to toggle as well, and so on. However, since there is always some small amount of propagation delay between the command to toggle (the clock pulse) and the actual toggle response (Q and Q' outputs changing states), any subsequent flip-flops to be toggled will toggle some time after the first flip-flop has toggled. Thus, when multiple bits toggle in a binary count sequence, they will not all toggle at exactly the same time:

As you can see, the more bits that toggle with a given clock pulse, the more severe the accumulated delay time from LSB to MSB. When a clock pulse occurs at such a transition point (say, on the transition from 0111 to 1000), the output bits will "ripple" in sequence from LSB to MSB, as each succeeding bit toggles and commands the next bit to toggle as well, with a small amount of propagation delay between each bit toggle. If we take a close-up look at this effect during the transition from 0111 to 1000, we can see that there will be false output counts generated in the brief time period that the "ripple" effect takes place:

Instead of cleanly transitioning from a "0111" output to a "1000" output, the counter circuit will very quickly ripple from 0111 to 0110 to 0100 to 0000 to 1000, or from 7 to 6 to 4 to 0 and then to 8. This behavior earns the counter circuit the name of ripple counter, or asynchronous counter.
In many applications, this effect is tolerable, since the ripple happens very, very quickly (the width of the delays has been exaggerated here as an aid to understanding the effects). If all we wanted to do was drive a set of light-emitting diodes (LEDs) with the counter's outputs, for example, this brief ripple would be of no consequence at all. However, if we wished to use this counter to drive the "select" inputs of a multiplexer, index a memory pointer in a microprocessor (computer) circuit, or perform some other task where false outputs could cause spurious errors, it would not be acceptable. There is a way to use this type of counter circuit in applications sensitive to false, ripple-generated outputs, and it involves a principle known as strobing.
Most decoder and multiplexer circuits are equipped with at least one input called the "enable." The output(s) of such a circuit will be active only when the enable input is made active. We can use this enable input to strobe the circuit receiving the ripple counter's output so that it is disabled (and thus not responding to the counter output) during the brief period of time in which the counter outputs might be rippling, and enabled only when sufficient time has passed since the last clock pulse that all rippling will have ceased. In most cases, the strobing signal can be the same clock pulse that drives the counter circuit:

With an active-low Enable input, the receiving circuit will respond to the binary count of the four-bit counter circuit only when the clock signal is "low." As soon as the clock pulse goes "high," the receiving circuit stops responding to the counter circuit's output. Since the counter circuit is positive-edge triggered (as determined by the first flip-flop clock input), all the counting action takes place on the low-to-high transition of the clock signal, meaning that the receiving circuit will become disabled just before any toggling occurs on the counter circuit's four output bits. The receiving circuit will not become enabled until the clock signal returns to a low state, which should be a long enough time after all rippling has ceased to be "safe" to allow the new count to have effect on the receiving circuit. The crucial parameter here is the clock signal's "high" time: it must be at least as long as the maximum expected ripple period of the counter circuit. If not, the clock signal will prematurely enable the receiving circuit, while some rippling is still taking place.
Another disadvantage of the asynchronous, or ripple, counter circuit is limited speed. While all gate circuits are limited in terms of maximum signal frequency, the design of asynchronous counter circuits compounds this problem by making propagation delays additive. Thus, even if strobing is used in the receiving circuit, an asynchronous counter circuit cannot be clocked at any frequency higher than that which allows the greatest possible accumulated propagation delay to elapse well before the next pulse.
Shift registers, like counters, are a form of sequential logic. Sequential logic, unlike combinational logic is not only affected by the present inputs, but also, by the prior history. In other words, sequential logic remembers past events.
Shift registers produce a discrete delay of a digital signal or waveform. A waveform synchronized to a clock, a repeating square wave, is delayed by "n" discrete clock times, where "n" is the number of shift register stages. Thus, a four stage shift register delays "data in" by four clocks to "data out". The stages in a shift register are delay stages, typically type "D" Flip-Flops or type "JK" Flip-flops.
Formerly, very long (several hundred stages) shift registers served as digital memory. This obsolete application is reminiscent of the acoustic mercury delay lines used as early computer memory.
Serial data transmission, over a distance of meters to kilometers, uses shift registers to convert parallel data to serial form. Serial data communications replaces many slow parallel data wires with a single serial high speed circuit.
Serial data over shorter distances of tens of centimeters, uses shift registers to get data into and out of microprocessors. Numerous peripherals, including analog to digital converters, digital to analog converters, display drivers, and memory, use shift registers to reduce the amount of wiring in circuit boards.
Some specialized counter circuits actually use shift registers to generate repeating waveforms. Longer shift registers, with the help of feedback generate patterns so long that they look like random noise, pseudo-noise.
Basic shift registers are classified by structure according to the following types:
- Serial-in/serial-out
- Parallel-in/serial-out
- Serial-in/parallel-out
- Universal parallel-in/parallel-out
- Ring counter

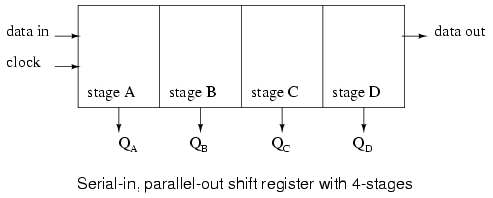
Above we show a block diagram of a serial-in/serial-out shift register, which is 4-stages long. Data at the input will be delayed by four clock periods from the input to the output of the shift register.
Data at "data in", above, will be present at the Stage A output after the first clock pulse. After the second pulse stage A data is transfered to stage B output, and "data in" is transfered to stage A output. After the third clock, stage C is replaced by stage B; stage B is replaced by stage A; and stage A is replaced by "data in". After the fourth clock, the data originally present at "data in" is at stage D, "output". The "first in" data is "first out" as it is shifted from "data in" to "data out".

Data is loaded into all stages at once of a parallel-in/serial-out shift register. The data is then shifted out via "data out" by clock pulses. Since a 4- stage shift register is shown above, four clock pulses are required to shift out all of the data. In the diagram above, stage D data will be present at the "data out" up until the first clock pulse; stage C data will be present at "data out" between the first clock and the second clock pulse; stage B data will be present between the second clock and the third clock; and stage A data will be present between the third and the fourth clock. After the fourth clock pulse and thereafter, successive bits of "data in" should appear at "data out" of the shift register after a delay of four clock pulses.
If four switches were connected to DA through DD, the status could be read into a microprocessor using only one data pin and a clock pin. Since adding more switches would require no additional pins, this approach looks attractive for many inputs.
Above, four data bits will be shifted in from "data in" by four clock pulses and be available at QA through QD for driving external circuitry such as LEDs, lamps, relay drivers, and horns.
After the first clock, the data at "data in" appears at QA. After the second clock, The old QA data appears at QB; QA receives next data from "data in". After the third clock, QB data is at QC. After the fourth clock, QC data is at QD. This stage contains the data first present at "data in". The shift register should now contain four data bits.

A parallel-in/laralel-out shift register combines the function of the parallel-in, serial-out shift register with the function of the serial-in, parallel-out shift register to yields the universal shift register. The "do anything" shifter comes at a price– the increased number of I/O (Input/Output) pins may reduce the number of stages which can be packaged.
Data presented at DA through DD is parallel loaded into the registers. This data at QA through QD may be shifted by the number of pulses presented at the clock input. The shifted data is available at QA through QD. The "mode" input, which may be more than one input, controls parallel loading of data from DA through DD, shifting of data, and the direction of shifting. There are shift registers which will shift data either left or right.
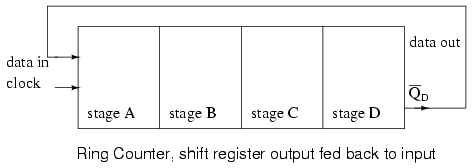
If the serial output of a shift register is connected to the serial input, data can be perpetually shifted around the ring as long as clock pulses are present. If the output is inverted before being fed back as shown above, we do not have to worry about loading the initial data into the "ring counter".
If the output of a shift register is fed back to the input. a ring counter results. The data pattern contained within the shift register will recirculate as long as clock pulses are applied. For example, the data pattern will repeat every four clock pulses in the figure below. However, we must load a data pattern. All 0's or all 1's doesn't count. Is a continuous logic level from such a condition useful?

We make provisions for loading data into the parallel-in/ serial-out shift register configured as a ring counter below. Any random pattern may be loaded. The most generally useful pattern is a single 1.

Loading binary 1000 into the ring counter, above, prior to shifting yields a viewable pattern. The data pattern for a single stage repeats every four clock pulses in our 4-stage example. The waveforms for all four stages look the same, except for the one clock time delay from one stage to the next. See figure below.
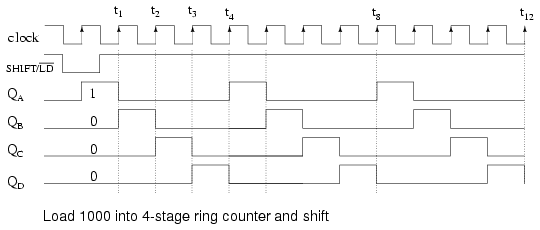
The circuit above is a divide by 4 counter. Comparing the clock input to any one of the outputs, shows a frequency ratio of 4:1. How may stages would we need for a divide by 10 ring counter? Ten stages would recirculate the 1 every 10 clock pulses.

An alternate method of initializing the ring counter to 1000 is shown above. The shift waveforms are identical to those above, repeating every fourth clock pulse. The requirement for initialization is a disadvantage of the ring counter over a conventional counter. At a minimum, it must be initialized at power-up since there is no way to predict what state flip-flops will power up in. In theory, initialization should never be required again. In actual practice, the flip-flops could eventually be corrupted by noise, destroying the data pattern. A "self correcting" counter, like a conventional synchronous binary counter would be more reliable.
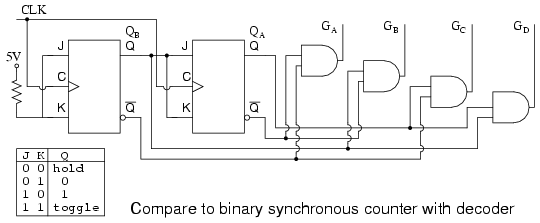
The above binary synchronous counter needs only two stages, but requires decoder gates. The ring counter had more stages, but was self decoding, saving the decode gates above. Another disadvantage of the ring counter is that it is not "self starting". If we need the decoded outputs, the ring counter looks attractive, in particular, if most of the logic is in a single shift register package. If not, the conventional binary counter is less complex without the decoder.

The waveforms decoded from the synchronous binary counter are identical to the previous ring counter waveforms. The counter sequence is (QA QB) = (00 01 10 11).
No comments:
Post a Comment